Pauli Exclusion Principle

No two electrons in an atom can have identical quantum numbers. This is an example of a general principle which applies not only to electrons but also to other particles of half-integer spin (fermions). It does not apply to particles of integer spin (bosons).

The nature of the Pauli exclusion principle can be illustrated by supposing that electrons 1 and 2 are in states a and b respectively. The wavefunction for the two electron system would be but this wavefunction is unacceptable because the electrons are identical and indistinguishable. To account for this we must use a linear combination of the two possibilities since the determination of which electron is in which state is not possible to determine.

The wavefunction for the state in which both states "a" and "b" are occupied by the electrons can be written
The Pauli exclusion principle is part of one of our most basic observations of nature: particles of half-integer spin must have antisymmetric wavefunctions, and particles of integer spin must have symmetric wavefunctions. The minus sign in the above relationship forces the wavefunction to vanish identically if both states are "a" or "b", implying that it is impossible for both electrons to occupy the same state.

Pauli Exclusion Principle Applications

Click on any of the bold text for links to further details.
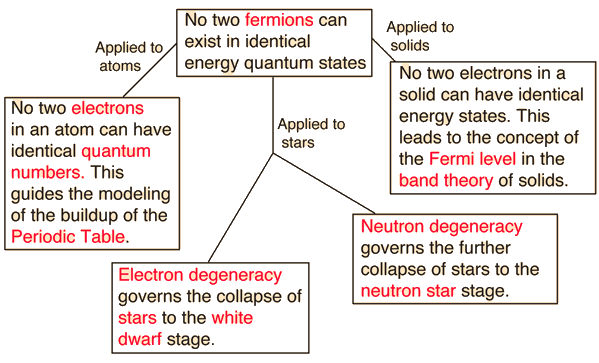
Read more...

"The Pauli Exclusion Principle states that no two electrons can have the same four quantum numbers. We are aware that in one orbital a maximum of two electrons can be found and the two electrons must have opposing spins. That means one would spin up ( +1/2) and the other would spin down (-1/2)

We have the first three quantum numbers n=1, l=0, m_l=0. Only two electrons can correspond to these, which would be either m_s = -1/2 or m_s = +1/2. As we already know from our studies of quantum numbers and electron orbitals, we can conclude that these four quantum numbers refer to 1s subshell. If only one of the m_s values are given then we would have 1s¹ (denoting Hydrogen) if both are given we would have 1s² (denoting Helium). Visually this would be represented as:

As you can see, the 1s subshell can hold only two electrons and when filled the electrons have opposite spins."

Read more...

More info...
About (dot) com